顧客と融資のご相談をしていると、
「利息ってどれくらいかかるの?」
「保証料ってどれくらいかかるの?」
「毎月の返済額は?」
などなど、必ずと言っていいほど聞かれます。
経営者の立場に立つと、利率〇〇%と言われても、それが実際の数値にしたらどれくらいのものなのか、許容できる範囲なのか、知りたいですし具体的な数値を元に交渉もしたいのです。
なので今回は、銀行員、経営者のための
融資の超基本的かつ意外と知らない「利息・保証料の計算方法」をご紹介します。
ただし、この計算式は元利均等方式の返済方法にのみ有効ですのでお間違えなく。
利息と保証料の計算
◯1円単位の毎月返済額を出したい場合
返済額(月)=借入額✖️{月利(1+月利)月数/(1+月利)月数➖1}
と言う計算式で導き出すことができます。
皆さんの言いたいことはわかります。
こんなの本番でやってられないよ!
せっかちな経営者もいるし、すぐに答えることで、出来る感をアピールしたいんだ!
そんな方の為に「分割係数」という主に保証協会で使われる考え方を使用して、毎月の返済額をざっくり出す方法をお教えいたします!
返済額(月)=借入額✖️年利✖️年数✖️0.55(分割係数)➕借入額➗月数
例えば、1000万円を5年借りて、利率1%なら、
毎月返済額=1000万✖️0.01✖️5年✖️0.55+1000万➗60ヶ月
=171,250円
となります。前半の分割係数までが全体の利息額で、後半が全体の返済額から毎月の返済額を導きだす計算となっています。
なので、利息額だけ知りたい!保証料だけ知りたい!と言う方は、前半(借入額〜分割係数)までを計算すれば、全体の利息額が算出できます。
また、0.55とは分割係数と呼ばれるもので、これは返済に応じて減った元金に対する利息額の減少を考慮するもので、返済回数が通常25回以上となった際に用いられる係数となっています。
返済回数が変われば分割係数も変わりますので、以下の表をご参考に、分割係数を変えて計算してみてください。
ただし、大抵2年以上のお借入だと思いますので0.55を使う回数が多くなります。最低でも0.55は暗記しましょう。
◯返済回数別の分割係数の目安(東京信用保証協会参照)
| 分割返済回数(月数など) | 分割係数 |
|---|---|
| 2回以上6回以下 | 0.70 |
| 7回以上12回以下 | 0.72 |
| 13回以上24回以下 | 0.66 |
| 25回以上 | 0.55 |
参照:東京信用保証協会分割係数のご案内
この計算式は、保証協会によっては正式採用されており顧客に対しても自信を持ってお伝えすることができます。
返済の種類

大別して「元利均等方式」「元金均等返済方式」があります。
元利均等返済とは
元利均等返済とは、毎月「同額返済」をする返済方式です。
そして、返済額に占める利息と元金の割合が期間の経過と共に変わります。
最初は残り元金が多いので、返済の大部分が利息に占められ、後半になるにつれ返済に占める元金の割合が増えます。
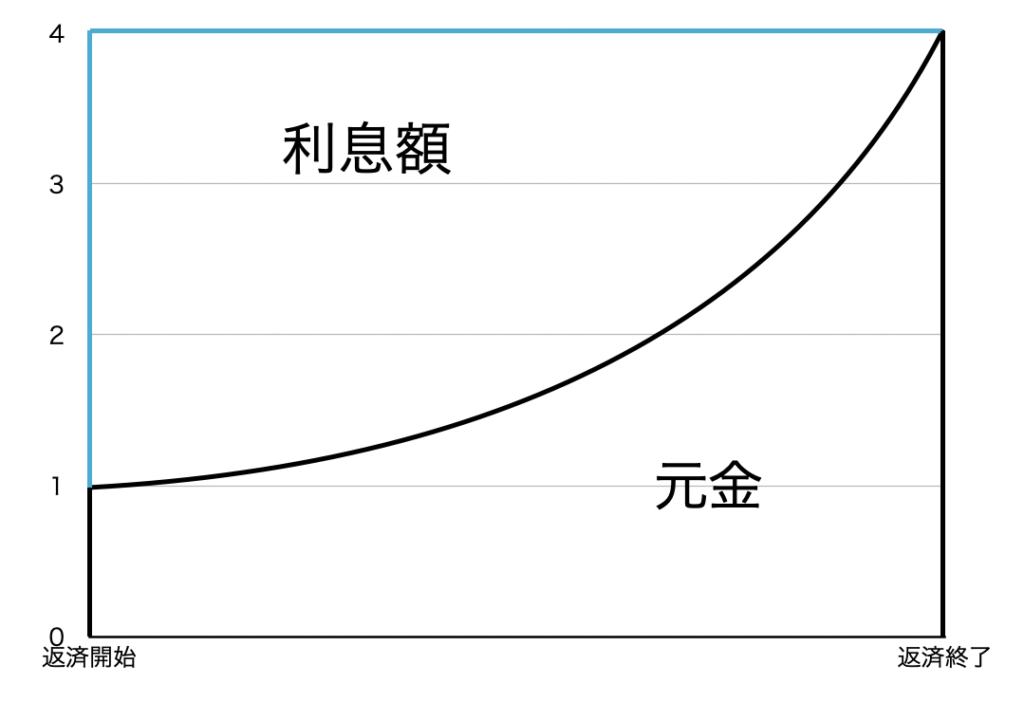
グラフをご覧いただければ分かるとおり、毎月の返済額は決められているので、最初の方は、多くの返済額が利息の支払いに充てられています。
メリット
・返済額が毎月同じで、返済計画が建てやすい
よくあるミスで、口座に入金する額を間違えた!
なんてことも毎月額が同じなので、ありません。
デメリット
・最初は利息の支払いが大きいので、最終的な返済額が増加すること
返済当初は、返済額の大部分が利息の支払いに充てられるので中々元金が減らず、返済額が大きくなってしまいます。
元金均等返済とは
元金均等とは、毎月「決まった元金額+利息」を返済する方式です。
元金額は、単純に
「合計➗返済回数」
です。
利息額は、残り元金の多い初めの方が大きくなり、元金の少なくなってきた後半の方が、少なくなります。
図で表すと以下のようになります。
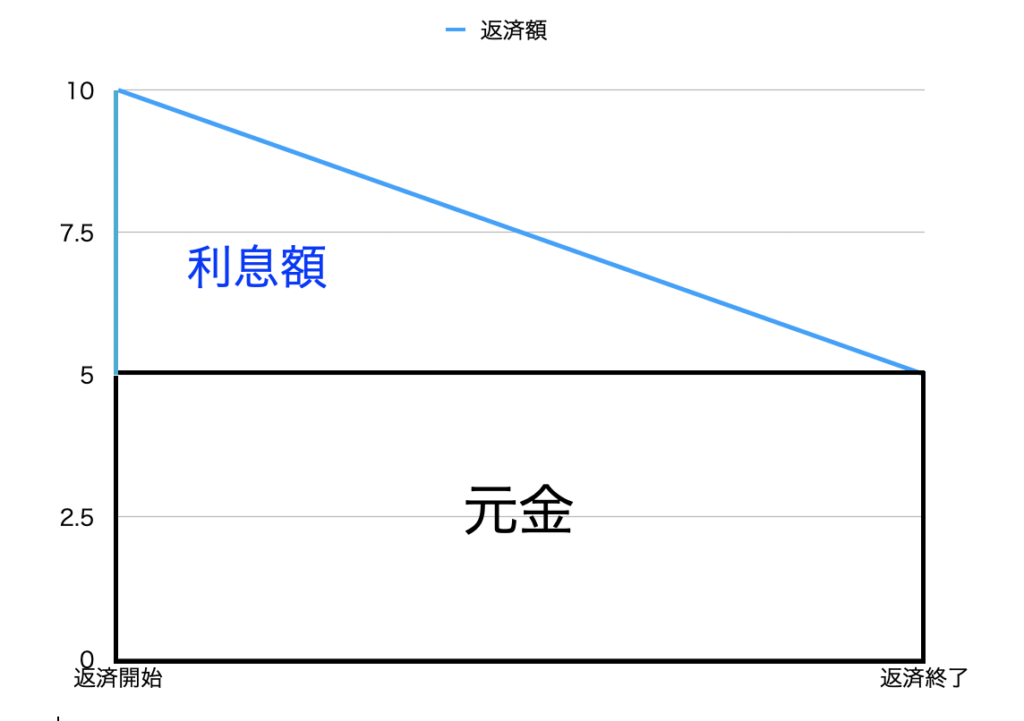
そして、この元金均等返済のメリット・デメリットは、
メリット
・最終的に返済額が少なくて済む
元金均等返済であれば、強制的に決まった元金を返済できるので、最初から大きく元金を減らすことができ、期間が同じなら最終的に返済額が減少します。
デメリット
・借入当初の返済額が多くなり返済負担が大きい
・返済額が月毎に異なる(減っていく)為、計画が建て辛い
と言うようなものになります。
主に住宅ローンなど、最初に返済余力がある方などが用いることが多いです。
まとめ

いかがでしたでしょうか?
保証料や利息の計算は、仕組みさえ理解すれば数秒で出来る様になります。
その場で、即座に計算し経営者の信頼を得る為にもぜひ覚えてください。
執筆者
T
現役銀行員
FP、簿記、保険、2種外務員、TOEIC、ビジネス法務..
などの資格と実務経験を持つ。
主に、銀行や金融の話題から、社会問題等に関する考察や説明を投稿していく予定。







